Quadratics of the form ax²+bx+c
I have been doing stuff with quadratics over the last few weeks, although I find some of it hard, I have understood most of it better than all the other content I have learned over the last few months.
So, I have now been learning how to solve a quadratic equation of the form
were a, b, and c are constants, if you can not factorize the equation then you can use a formula
To solve the quadratic equation find the constants so, a=1 (because it is
b=6 and c=1.
If I sub these in to the following formula.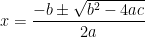

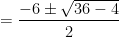
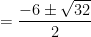
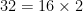
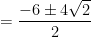
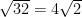
so the solutions to this equation are...
and

I do have another quadratic equation to solve in the same sort of way, I will add that in the next couple of days. Making sure all the typesetting for the equations is correct takes a bit of time of which I have very little nowadays.


